(Teorema de Papus para a elipse). Considere o conjunto A de todos os pontos (x, y) tais que
E situado no semiplano Mostre que o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto A é igual ao produto da área da elipse pelo comprimento da circunferência gerada, na rotação, pelo centro desta elipse.
Passo 1
Calma! Relaxa! Esse monte de letra tem algum significado e eu vou te mostrar.
Primeiro temos que entender o gráfico com equação:
Essa equação representa a circunferência de raio 1 centrada na origem.
Quando deslocamos o centro da circunferência para um ponto , ficamos com:
Até aí tranquilinho? Show!
E, no caso da elipse, como ela não tem os tamanhos iguais, ficamos com:
Ficamos com esse gráfico:
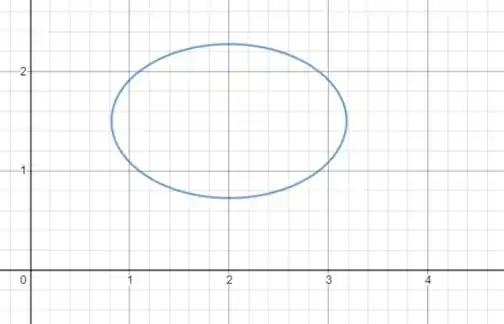
Gráfico genérico de:
Ok! Agora entendemos que essa relação é de uma elipse, e que a e b devem ser valores positivos.
Mas por que esse valor “”?
Por que ele pede pra considerarmos apenas o conjunto A de pontos (x, y), ou seja, pontos que obedeçam a essa regra. Resumindo: ele quer a área que está dentro da linha que descreve a elipse.
Mas ele pede que . Então ele quer que a gente use a área entre a curva que descreve a elipse acima do eixo x e o próprio eixo x. Ou seja, isso aqui:
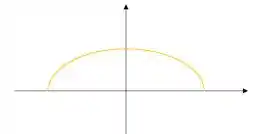
Ótimo! Entendemos o que quer dizer esse monte de letra e essa relação, mas afinal de contas o que o exercício pede?
O exercício nos pede para comparar duas coisas:
1 – O volume do sólido obtido pela rotação, em torno do eixo x, do conjunto A;
2 – O produto da área da elipse pelo comprimento da circunferência gerada, na rotação, pelo centro desta elipse.
Sendo assim, conhecemos métodos para realizar essas duas operações e em seguida comparamos os resultados para ver se batem.
Passo 2
Pelo teorema de Pappus-Guldin sabemos que para volumes usamos:
Sendo a r a circunferência em relação ao eixo e A é a área da elipse.
A área da elipse é descrita por:
Logo a Área da semi-elipse é metade disso.
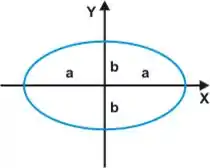
E a distância entre o centro da semi-elipse acima do eixo x e o próprio eixo x é dada sempre como na circunferência.
Imagine que nós tenhamos apenas um semicírculo acima do eixo e rotacionamos essa figura em relação ao eixo x,
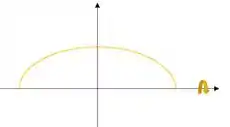
Vamos ter o volume da esfera que é:
Passo 3
Então, se compararmos com o teorema de pappus-Guldin, teremos:
E sabemos que que a área vale então ficamos com
Sendo o do teorema de Pappus-Guldin o centroide da figura, se colocarmos o centroide em evidencia (lembrando que a área da semicircunferência é ) , teremos:
Então temos que
Assim ficamos com:
Passo 4
Para calcular o volume do sólido obtido pela rotação, em torno do eixo x, do conjunto A usamos a fórmula:
Para usar esse método precisamos de e dos limites de integração.
A função depende de x, logo vamos isolar :
Passando para o outro lado, ficamos com:
Agora vamos deixar apenas o termo que tem do lado esquerdo,
Ajeitando isso ai ficamos com:
Ok então temos que:
Como a elipse está com centro no eixo x, temos,
Passo 5
Pelo gráfico podemos ver que x varia de até , então o intervalo vai ser:
Tirando as constantes para ficar menos complicadinho, vamos ter:
Agora vamos separar em duas integrais
Vamos fazer uma substituição simples e chamar de , nisso nossos limites de integração mudam, quando e quando
Agora resolvendo esse monstrinho ai ficamos com
Dando um jeitinho, ficamos com
Ufa! Assim comparando os valores encontramos que o volume pode ser representado dessas duas maneiras
Por pappus-Guldin ou por sólido rotacional.
Resposta
Ei, a resposta está no passo a passo :)